You can dig a hole into my soul which is hollow like a bowl.: perseus

Matematycznie ścisłe sformułowanie mechaniki kwantowej pochodzi od Paula Diraca i Johna von Neumanna. W tym sformułowaniu stan układu kwantowego (stan czysty) reprezentowany jest przez wektor jednostkowy (nazywany wektorem stanu) w zespolonej przestrzeni Hilberta (nazywanej często przestrzenią stanów układu fizycznego).
Każda wielkość fizyczna (obserwabla) reprezentowana jest przez hermitowski (lub samosprzężony) operator liniowy działający w przestrzeni stanów (przestrzeni Hilberta). Zbiór wartości własnych tego operatora, nazywany widmem punktowym operatora, interpretujemy jako zbiór możliwych wartości obserwowalnych (pomiarowych). Dla hermitowskich operatorów wartości w widmie są liczbami rzeczywistymi co stanowi motywacje ich wprowadzenia w takiej a nie innej roli. Stany własne tego operatora do tych wartości własnych interpretujemy jako możliwe stany, w których znajdzie się układ po dokonaniu pomiaru.
Alternatywnym sformułowaniem jest feynmanowskie funkcjonalne całkowanie po trajektoriach. Jest to odpowiednik zasady najmniejszego działania w mechanice klasycznej.

linka-szklanka
pękła jak sztywna bańka
irytujący dźwięk świateł dla pieszych zamienił się w kardiogram
pik-pik
rozbite szkło w sukience
zdjęło sukienkę, nie zasługuję na sukienkę
pik-pik

No one's picking up the phone
Guess it's clear he's gone
And this little masochist
Is lifting up her dress
Guess I thought I could never feel
The things I feel
Hey Jupiter

płacz, maleńka pęknięta szklanko, płacz jak żeś głupia

Thought I knew myself so well
All the dolls I had
Took my leather off the shelf
Your apocalypse was fab
For a girl who couldn't choose between
The shower or the bath

problem w tym, że bez tego moje życie byłoby pustką
pustką bez "odśwież" ślad w witrynie
pustką bez czekania na spotkanie na ulicy
pustką bez pamiętania układu żył na przegubie

If my hearts soaking wet
Boy your boots can leave a mess

brudzę się o siebie
o trzymaną kurczowo nitkę pełną smaru
owija się wokół szyi, a ja dalej trzymam

linka- szklanka
desperatka, szachrajka, nudna makatka

la stanu czystego reprezentowanego przez wektor $|\psi\rangle$ odpowiadający mu operator to

$\rho=|\psi\rangle\langle\psi|$ ,

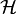czyli operator rzutowy rzutujący na jednowymiarową podprzestrzeń $|\psi\rangle$ przestrzeni Hilberta $\mathcal{H}$ .
Z kolei dla stanu mieszanego składającego się z (nieinterferujących ze sobą) składników $|\psi_i\rangle$ odpowiadający mu operator gęstości to

$\rho=\sum_{i} \lambda_i|\psi_i\rangle\langle\psi_i|$ ,

gdzie

λ i

to prawdopodobieństwa znalezienia poszczególnego składnika. Muszą one spełniać $0\leqslant \lambda_i<1$ dla każdego i oraz

∑	λ_i = 1.
i

Jest to operator o wartościach własnych

λ i

stowarzyszonych (odpowiednio) z wektorami własnymi $|\psi_i\rangle$ .

Dzięki temu, że powyższe równanie jest liniowe, w wyprowadzeniu można ograniczyć się do stanów czystych. Istotna jest także samosprzężoność hamiltonianu.

$\frac{\partial |\psi\rangle\langle\psi|}{\partial t} = \frac{\partial |\psi\rangle}{\partial t}\langle\psi| +|\psi\rangle\frac{\partial \langle\psi|}{\partial t} =(\frac{1}{i \hbar}\hat{H}|\psi\rangle)\langle\psi| +|\psi\rangle(\frac{1}{i \hbar}\hat{H}|\psi\rangle)^*$

2 komentarze:

...24 lipca 2011 21:18
nie wylewaj ich na darmo..prześlij mi te krople..
OdpowiedzUsuń
Odpowiedzi
Romsi26 lipca 2011 12:22
Oj, oj, niedobrze z Tobą. Co Ty czytasz szosztro?! Nagle Ci się odmieniło na fizykę? Straszne! Wektory nie prowadzą donikąd! Wiem co mówię! :*
OdpowiedzUsuń
Odpowiedzi

Dodaj komentarz

niedziela, 24 lipca 2011

perseus

2 komentarze:

.